Aethodian conventions
Theodia, being largely an engineered society, has a number of conventions that differ radically in many ways from those in use in the rest of the world. Most of the systems relating to how we measure and describe the world have been redesigned from the ground up to be more ergonomic and intuitive, as well as to work better with each other. This article details these conventions, and was current as of 2021, May. Note that some sections will not make much sense if read out of order.
Language
The Theodian language, being an engelang (an engineered conlang), has been schematically designed, with its goal being akin to those of the other systems in use in Theodia: to be as ergonomic, intuitive, and consistent as possible. It has innumerous features deserving of mention in this light, and these are all mentioned within its own article rather than here, for the sake of modularity. Of particular import to the understanding of the following sections, however, is the knowledge that the Theodian language uses base-twelve for its numbers, and that it is written from bottom-to-top-to-bottom-then-left-to-right-ly.
Measurement
Theodia has long had its own system of measurement, named the Ergonometric system; it was designed to strike a balance between anthropic ergonomics (relatability of the units to everyday human use), metricality (regularity in scale and interrelation of the units), and naturality (basis of the units in some fundamental constants). The current system uses a duodecimal base, due to its advantages over decimal; and is compatible with the Universal Unit System due to normalizing the following constants to 1: R∞ (the Rydberg constant), c0 (the speed of light in a vacuum), (the quantum of action), kB (the Boltzmann constant), NA (the Avogadro constant), and R (the gas constant). Normalizing these constants and scaling them by integer powers of twelve, results in a natural unit system that can integrally approximate virtually every important physical constant to within nearly 1% of either its actual value or some proxy for that value (such as half of the constant). However, certain units are modified from or derived entirely separately from their UUS equivalent, for the sake of usability.
The signifiers for each unit start with a Metric base-unit equivalent, and end in e (for 'Ergonometric'). When a unit needs scaling in one direction or another, scientific notation is used, eg: n(104)me. In-keeping with Theodian's use of myriads rather than thousands, exponents are usually multiples of four. As such, this is closer to engineering notation than scientific notation.
- Distance
The unit of distance is known as the "Ergo-Meter", or me, and is defined as ? (approximately 2.2696cm, or 0.8935in).
Before the adaptation of the Universal Unit System in mid-2017, several other suggestions were made for the distance unit; ultimately, none was deemed sufficiently ideal, for one reason or another. The most notable was basing the standard unit off the average stride length of an adult human. Using a value of 78cm as suggested by one study yields canonical values for unit/twelve and unit/gross, and directly relates a distance to the number of steps required to walk it; but, as with many bodily metrics, there is great variation between people. Another idea was to base the Ergo-Meter off of average body-part sizes, which could have facilitated approximate measurement; but this fell ill to the same limitation. Another was to use the smallest DPI at which the dots are still visible to an unaided eye, and multiply it by twelve until it was conveniently sized. The problem with this suggestion, was that that particular DPI varies between people and by distance from the item being viewed.
- Volume
The unit of volume is known as the "Ergo-Liter", or le, and is equal to the volume of a cube with all dimensions equal to the Ergo-Meter (approximately ?ml, or ?floz).
For quite a while, the unit of volume was taken as the most basal unit, with distance being derived from it. During this time, it was equal to the average volume of liquid a human consumes in a single swallow, which (according to one source[1]) is about 16ml under normal conditions; but there is unfortunately great variability in amounts swallowed, as shown in other studies[2][3], which makes it difficult to name a particular volume as a "Standard Swallow". This unit, had it been feasible, would have had the unique benefit of allowing one to tell, just by looking at a drink's volume, approximately how many times se'd've be able to have drink from it.
A previous suggestion for the unit of volume was the average amount of liquid holdable in a single person's mouth. However, it was later decided to base the volume off the average amount swallowed, as not only was there very little data on the average capacity of our oral cavities, but using the average amount swallowed more closely relates to what we're doing when we hold liquid in our mouths.
- Mass
The unit of weight is known as the "Ergo-Gram", or ge, and is defined as ? (approximately ?g, or ?oz).
Before the adaptation of the Universal Unit System as a backend, the unit of weight was based on the weight of water at sea-level and at body-temperature with a volume equal to the Ergonometric volume unit. Water was chosen due to its Earthen ubiquity and anthropic import.
- Pressure
The unit of pressure is known as the "Ergo-Bar", or be. It is epoched to 101.325kPa (kiloPascals), the average pressure at sea level[4] on Earth; and it is defined as ? (approximately ?Pa).
- Temperature
The unit of temperature is known as the "Ergo-Kelvin", or Ke. It is epoched at the human body's core temperature, which is 37°C; and it is defined as ? (approximately ?°C), as the average amount of daily core temperature fluctuation in the human body is about 0.5°C. This makes all temperatures instantly relatable. For example, room temperature is -24Ke (remember that the Ergonometric system uses base-twelve, meaning that the decimal representation of this would be -28Ke).
- Radial degrees
Whereas in the West, 360° decimal is the conventional total of arbitrary subdivisions of a circle; in Theodia, 4° dozenal, inspired by the gradians system, is used. 4° dozenal is a more sensible total than 260° dozenal (360° decimal) and 1° dozenal because:
- Dozenal, being highly divisible, doesn't suffer the same weaknesses as a decimal gradians system, and so a highly divisible auxiliary base (like 360) is not needed (the main reason why a gradians-esque system is rather limited under a decimal regime, and why no decimal society has
100°per circle). - There aren't 360 days in a year (this was the original rationale for using
360°). - Using
4°makes every degree-measure tell you its quadrant.x.y°, for example, would be in quadrantx, as well asy0%of that quadrant. - Using
4°makes it easier to subdivide a fourth of a circle than using1°or100°. - Using
4°relates degree-measures to tau'd radians very clearly, as3°, for example, is3τ/4(3Ͳin sampi'd radians). - The number of degrees in a polygon is equal to the number of sides it has, such that a pentagon, for example, contains
5°.
- Time
The Ergonometric system has two standards for time, those being, respectively, the duration of an Earthly day, and the duration of a human's daily circadian rhythm. Although these are the same in duration, one is inherently circular, while the other has no physical shape. Because Theodia's official calendar is decoupled from other external processes, the latter format is more common within Theodia; but the former format has the advantage of being identical to the number of degrees the Earth has rotated.
The former system divides each day into four parts, treating the day like a circle (and thus making each unit of time equal to one degree of the Earth's rotation). This is essentially four hours per day. A radix-point is then introduced for finer values. Using four hours per day gets all the same advantages of using 4° in a circle. In particular, however, the quadrants correspond with midnight, equinoctal dawn, noon, and equinoctal dusk. Times are typically carried out to two post-radix-point significant digits, as this gives a comparable, but still lesser, fineness to conventional minutes (with each "minute", per se, lasting about twice as long as an ISO minute). A less fine minute-length was desired so as to make schedules a little more forgiving.
Here is a formula for converting between ISO time and radial Ergnonometric time: Plug in the ISO values of hour, minutes, and seconds here: (h + m/60 + s/3600) / 6, then paste the result into a decimal-dozenal converter, such as the one available here. An Ergonometric hour lasts for six ISO hours, one-twelfth thereof for thirty ISO minutes, and one-twelfth thereof for 2½ ISO minutes.
The latter system divides each day into twelve parts, so that the time can easily be stated in radices involving days, weeks, years, etc. Under this system, there are essentially twelve hours per day, each lasting for two ISO hours. This can, of course, be further subdivided ad infinitum. All that need be done in order to convert an ISO time-value into a linear Ergonometric value is to state it in terms of hours, divide by two, and convert to dozenal.
Here are some examples of ISO time in relation to both radial and linear Ergonometric time:
- ISO:
13:45, Ergonometric (radial):2.36°, Ergonometric (linear):6.26 - ISO:
17:30, Ergonometric (radial):2.30°, Ergonometric (linear):8.90 - ISO:
21:15, Ergonometric (radial):3.66°, Ergonometric (linear):3.76
Sizing
This section details the various official sizing conventions currently in-use in Theodia. Wherever possible, standard sizes are integers of their respective Ergonometric unit. All numbers are written in dozenal.
- Fabric
- Standard flag:
6me * (l * w)
landwdepend upon the ratio of the flag in-question. Using Theodia's national flag as an example, a ratio of7:4results in a flag of38me * 20me.
- Masonry
- Standard mortar thickness:
½me
- This is very close to thicknesses used in Western masonry, while remaining compatible with Theodian units.
- Standard brick:
3me * 3me * 2me
- These dimensions were designed to allow standard bricks (1) to be compatible with the Theodian bond (which requires bricks with a
1:1:3ratio when drystacked), and (2) to be easily manipulated by a single hand. The reason that the long axis is2meinstead of9me, is so that there is room for mortar at the standard thickness. - Although
2is not a very dozenal-friendly distance, no other basic integral size (2or4) was any better than3at producing a useful post-mortar length, and3me * 3meis already very well-suited to the hand. The good news, however, is that, when using the Theodian bond, measurements can be planned with alternating sections of long and short mortared bricks, which provides a minimal section length of12me, which is a bit easier to work with.
- Standard block:
2me * 2me * 27me
- The standard block size was designed to allow standard blocks (1) to be compatible with the Theodian bond (which requires blocks with a
1:1:3ratio when drystacked), (2) to be small enough to be realistically manipulable by a single person using both ser hands, and (3) to be compatible with standard Theodian bricks (Each of a block's dimensions is the size of 3 bricks mortared together.). The reason that the long length is27meinstead of23meand the other lengths are2meinstead of9me, is so that there is room for mortar. - Although
2and27are not very dozenal-friendly distances, these numbers were required in order to be compatible with the standard bricks. The good news, however, is that, when using the Theodian bond, measurements can be planned with alternating sections of long and short mortared blocks, which provides a minimal section length of36me, which is much easier to work with.
- Publications
- Standard copy paper:
8me * 6me(landscape)
- This takes the most popular tablet length (
7"as of 2013[5]) (Tablet sizes were used, because tablets, being heavier than paper but held much the same way, provide a unique case study in human holding preferences.), puts it into a4:3ratio (as this approximates the natural field of view of a human eye[6]), expresses them in integral Ergonometric terms, and uses them to define the size of a standard sheet of copy paper. Landscape is generally used in lieu of portrait, because vertically written scripts (like Theodic) fare better on a landscape medium.
- Standard notecard:
4me * 3me(landscape)
- This takes the most popular smartphone diagonal (
120mm(4.7") as of 2015[7]) (because phones are generally held in one hand, like a notecard), applies a landscape4:3ratio to it (for the same reasons that a landscape4:3ratio is used for the standard copy paper size), and expresses the resulting dimensions in integral Ergonometric terms. Conveniently, this results in a notecard size that is a divisor of the standard copy paper size.
- Weaponry
- Standard arrow:
28me
- This is between the fabled clothyard shafts of mediæval England, and the shafts of today's Olympic archers.
Mathematics
- Order of operations
Theodia uses PEMDAS, as it is already quite sensible.
- Constants and variables
As these are inherently arbitrary, Theodia has not reformed any of the conventional Western symbols for mathematical constants and variables. As an additional reason for its use of Latinate variables, Theodic numerals are identical to Theodic letters, leaving almost only the vowels as potential native variables.
- Logical and numerical bases
The Theodian language (and, consequently, Theodia) conventionally uses a three-valued logic (balanced ternary, in this case), because:
ehas the lowest radix-economy and rounds to 3, making 3 have the lowest radix-economy for an integer. This makes ternary more efficient at encoding data than binary.- Three-valued logics are better-equipped to describe quantum systems.
The Theodian language uses base twelve for its numbers, as opposed to the more common base ten. The use of dozenal (base twelve) over decimal (base ten) confers upon Theodians a unique ease in performing proportional mathematical operations, as dozenal makes the radix-notations (the "decimal" points) of fractions like 1/3 and 1/4 incredibly simple, and it also has an easier multiplication-table than decimal. The Dozenal Society of America has a number of articles explaining in greater depth dozenal's superiority to decimal.
- Coordinates
Theodia uses the order of (y,x) in the denotation of 2D points, since:
- Theodian is, at least by default, written BtTtB-LtR, so a Theodian, when looking at the all-positive quadrant of a Cartesian plane, would see the
y-axis first, and the natural direction for the script to go after going up would be to go right. - Having
ycome first and other coordinates follow it means thatyis the only coordinate in 1D space. This automatically gives all 1D lines an undefined rise/run slope (as ally-axis 1D lines are vertical), which makes sense given that slope is a meaningless concept in 1D space. - Climatic conditions on conventionally rotating heavenly bodies correlate only with the
y-axis, which makes it more relevant than thex-axis.
Because the (y,x) format is used, the default slope-intercept equation in Theodia is y = mx + b, so that m will have the format of (y / x), or "Rise over Run". This is convenient, because "Rise over run" not only makes literal sense and intuitivizes vertical 1D space, but matches the writing-direction.
In the denotation of coordinates in systems with dimensions greater than two, the relevant values are appended to the basic (y,x) convention, such that coordinates in a 3D space would have the format of (y,x,z).
Note that these variables no longer present themselves in alphabetical order. This could be resolved by simply swapping x and y's meanings for each other's. However, since the Latin alphabet is not the main writing-system for the Theodian language, and as Theodia conventionally leaves the traditional symbols for constants and variables alone, the definitions of x and y have been left as-is.
- Circles
Theodia also uses a starting-point and direction for circles which is different from the norm in the West. Whereas it is more conventional in western society to start an origin-centered circle from the right half of the x-axis, and thence move counterclockwise; in Theodia, it is conventional to start an origin-centered circle from the bottom half of the y-axis, and thence move clockwise. There are numerous reasons for why this was chosen to be the case:
- In BtTtB-LtR (bottom-to-top-to-bottom, left-to-right) writing systems, of which Theodic is one, circles spin clockwise (this directionality was also chosen in part for compatibility with a clockwise base).
- In the northern hemisphere of the Earth, where the majority of humans live and where the majority of the land-mass of the Earth is located, the sun appears to traverse the sky clockwise, as it rises in the East, sits in the South, and sets in the West.
- Because of this, not using a clockwise orientation would confound sundials in the northern hemisphere.
- Cartesian plane
In keeping with the directionality of circles, Cartesian planes' quadrants are, in Theodia, numbered clockwise from the bottom-left, starting from 0 (for compatibility with the degrees system), such that the all-positive quadrant is quadrant 2.
- Radians
For radians, Theodia uses τ/4 in mathematical instruction, with the nonstandard mathematical symbol Ͳ, archaic Greek sampi, having been chosen to represent this, due to its being something of a graphical admixture of <τ> and <π>. Generally speaking, Ͳ is best when the degree-count is gradian-like (as Ͳ is the ratio to one-fourth of a circle), and τ is best the rest of the time (as τ is the ratio of an entire circle, and so is compatible with any degree-count). As Theodia uses a gradian-like degree-count (a 4° total, in this case), Ͳ becomes more intuitive, resulting in radians and degrees that are always identical (ie, 1.1° is 1.1Ͳ). Because of this, one of the systems can be forgone. In Theodia's case, this is degrees, which has been completely replaced by radians, since the degrees symbol, ° is similar to 0, and could be mistaken as taking the 0th power of something; while the radians 'symbol' (Ͳ) follows typical mathematical conventions for units.
As well, while τ simplifies many formulas, it still complicates a few (eg, πr2, which becomes τr2/2). Ͳ adds minimal complication (the previous example becomes 2Ͳr2) in all cases, since it is smaller than π.
In Theodic, the writing style represents <Ͳ> like <ш> (inverted Cyrillic sha), and the carving style like <ᛏ> (akin to Gothic sampi).
- Trigonometry
In an effort to ameliorate much of the difficulty surrounding trigonometry, Theodia has adopted a more intuitive set of conventions, in a addition to simply merging radians, degrees, and hours. In Theodia, the three basic trig' functions are not sin, cos, and tan; but, rather, cos, csc, and tan, in that order (which places the signifiers into alphabetic order in the Latin alphabet). As well, the mnemonic for remembering them is, in Theodia, not "SohCahToa"; but, rather, "hoahoa", at least in English -- although placing cosine, cosecant, and tangent in that particular order will, in any language, generate a set of three phones reduplicated once, making this mnemonic universally applicable. Further, Theodia does not typically use terms such as "sine", "secant", and "cotangent", as cos:sec::csc:sin is counterintuitive; preferring instead to simply represent them as the reciprocal of their reciprocal functions. Additionally, choosing cosecant, cosine, and tangent instead of any other functions results in each side being in the numerator only once, which can, itself, be a kind of mnemonic. Beyond all of this, Theodia conventionally proscribes denoting sin(x)y as siny(x), as the latter is not generally the convention elsewhere in mathematics, and so can be confusing to the uninitiated.
It is possible to get the same benefits by using secant, sine, and cotangent, which would have the mnemonic "haohao"; but doing this does not place them into alphabetical order, and complicates tangents, which have a literal meaning that sines and secants don't have, especially in Theodia where circles open at a different place than in Western math.
Rational trig was considered, but ultimately decided against, as its focus on quadrance over distance is unintuitive, and its focus on spread over angle adds an extra parameter to math and breaks apparent compatibility between circular and polygonal geometry.
Cartography
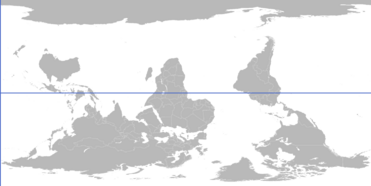
- Earthling continents
Theodia uses a hybrid continent model for the planet Earth, having the following 2 supercontinents: Afro-Eurasia and Antarct-America; and the following 6 continents: Africa, Antarctica, Eurasia, North America, Oceania, and South America. Theodia also divides the various continents into subcontinents, with Eurasia, for example having the following subcontinents: Chukotko-Kamchatka, East-Eurasia, Europe, Greater Arabia, Greater India, Greater Indochina, and Greater Siberia. Africa has East, Madagascar, North, South, and West. Oceania has Australia, Eastern Polynesia, and Malaya. North America has Greater Appalachia, Greater Cascadia, Greater Mexico, Greater Nunavut, The Caribbean, and The Great Plains. South America has Amazonia, Rioplata, and The Andes.
Continents, in Theodia, are largely physically delineated, whereas subcontinents are largely cultural and historical, with a preference for physical delineation where possible.
- Meridians and parallels
Theodian maps of Earth typically use the Florence antimeridian (located at 168°45'W in the Greenwich system, or M+0Ͳ in Theodia (with 'M' standing for 'Meridian')) as their prime meridian. The Theodian system uses for longitude a single continuum from M+0Ͳ to M+3.3Ͳ across the whole globe, in contrast to the Greenwich system, which uses the conventions of °W and °E for the halves of the globe on either side of the prime-meridian. The signifier 'M' comes first in Theodia, as the degrees are technically being added to or subtracted from the prime meridian or prime parallel, rather than being multiplied by it (this distinction is particularly important in Theodia, where degrees have been completely replaced by radians).
For latitude, the Theodian system has its prime parallel at the Equator, with the northern pole at P+1Ͳ (with 'P' standing for 'Parallel'), and the southern pole at P-1Ͳ; in comparison to the Greenwich system, which goes up to 90°N and down to 90°S.
A continuous system was chosen for longitude because there is no natural prime meridian on a globe, and it was not desired to make Theodians use a system that pretends there were; and a centered system was chosen for latitude because there is a natural prime parallel (which is the equator) (and, coincidentally, this increases compatibility with Theodia's timeline-format, whose labels are placed above and below a horizontal line).
Theodian cartography still has the concepts of Western and Eastern hemispheres, but unlike the Greenwich system, they are not central to it (although some maps seeking to have at their centers in the Pacific rather than in the Atlantic will often start the map from the eastern boundary of the western hemisphere. In Theodia, the western hemisphere is taken as going from M+¿?Ͳ to M+?¿Ͳ (about 154°45'E to 25°15'W under the Greenwich system), and the eastern hemisphere as going from M+?¿Ͳ to M+¿?Ͳ. These were defined as they were, so as to create reasonable lateral hemispheres, in this case doing so by separating the New World from the Old.
- Projections and orientation
In the absence of a globe, the projection recommended for general use is an orthographic azimuthal projection (as it is essentially akin to viewing a portion of a globe); but use of projections where a globe would suffice is discouraged (per the 1989 resolution). Regardless, the preferred cylindrical projection is a simple equirectangular projection with a standard parallel of 30°N (P+0.4Ͳ) (this reduces overall distortion), as it is easy to convert pixels into coordinates with such a projection.
Theodian maps typically display south-up. The reasons for this have nothing to do with those which Gall and Peters had, but rather have to do with being as consistent as possible with other systems used in Theodia:
- A south-up orientation for the Earth, especially given the coordinates-system used in Theodia, is the orientation most compatible with the timeline-format used in Theodia, as it causes the Earth to rotate left-to-right, rather than right-to-left.
- It makes the Earth, from the "top" (now the south), appear to rotate clockwise, and to revolve clockwise around the Sun. This is the rotative direction most compatible with the other rotative systems in Theodia, such as the directionality of circles and the Cartesian plane.
- A west-up globe would not allow for a compatible view of the overhead solar-system, as it would display the entire solar system along its thinnest axis.
- It provides more intuitive metaphors, since (for most of the world's population) going 'up' (south) generally increases the ambient temperature, and going 'down' (north) generally decreases the ambient temperature (This reflects the reality that buoyancy increases with heat.).
This system is extended for other heavenly bodies, such that:
- All solar systems are seen as moving clockwise; and
- Planets have their 'top' at whichever pole would make the planet appear to spin left-to-right.
Charts
- Calendar
The Theodian calendar, often referred to as the 'Kalendar' in writing, is the official calendar of Theodia for both civil and fiscal purposes. It differs radically from the Gregorian calendar. Theodian years, for example, are 144 days long and completely decoupled from Earthly cycles. Standard formats for date-representation are all little-endian, like ISO dates.
- Timelines
Timelines display from left-to-right, with labels going either from bottom-to-top above the line, or top-to-bottom below it. This maximizes consistency with the writing-direction of Theodian (BtTtB-LtR) and the system of coordinates used for planets.
Traffic
Theodian traffic laws are also highly engineered, comprising innumerous tweaks and things designed to make driving as safe and convenient as possible. They are many enough that they necessitate their own article, but summarily, it is most important to know that Theodia uses left-hand traffic, has roadsigns based upon positive contrast, speed-targets rather than speed-limits, and singleton traffic-lights.
Chirality
- Stadia-directionality
Stadiums, in Theodia, race in a clockwise direction, rather than in a counterclockwise direction, as is common elsewhere. This is not only maximally compatible with the other systems in-use within Theodia (which are all based upon clockwise orientation), but also maximally compatible with Theodia's use of left-hand traffic (which naturally results in clockwise roundabouts).
Jousting and horse-archery, however, get shafted a bit, because they almost necessarily require moving counterclockwise, due to the shield and the bow most commonly being held in the left hand. However, no system is maximally compatible with everything, and these sports will simply have to exist as exceptions to the clockwise rule. It is also worth noting that not all forms of mounted combat prefer a counterclockwise movement: shieldless lancework, any swinging weapon, and pistols all prefer a clockwise direction from horseback.
- Threadedness
The threads of a right-axle screw, in Theodia, are conventionally such that the screw turns clockwise (when looking at it from the top) when entering an object, and counterclockwise when exiting -- as is the convention elsewhere. There doesn't appear to be much difference in ease when operating a screwdriver one way or another[citation needed], so a clockwise orientation makes the most sense, given the other systems in-use in Theodia.
- Fans
In Theodia, ceiling-fans, when blowing air downwards, appear to spin clockwise for an observer located below the fan. This is because a fan which blows downward, pushes itself upwards; and, since, from the top, a clockwise fan appears to rotate counterclockwise, this directionality closely parallels that of threads: both are spinning in some medium, and both move upwards when spun counterclockwise. To not use this such a directionality for fans, given the systems used elsewhere in Theodia, would be a significant source of irregularity. Elsewhere in the world, not only do ceiling fans spin counter to the dominant threadedness, but non-ceiling fans often do follow the dominant threadedness, thus adding yet another inconsistency to the puzzle.
Additionally, it is traditional for Theodian ceiling-fans to have 3 or 4 blades. 3 blades is the smallest number which maintains stability in turbulence (a 2- and 1-bladed fan can tilt, due to having angles at or greater than 180°); and a 4-bladed fan is the easiest-to-construct stable fan.
- Round-robin
Round-robin systems should always progress from smallest to largest. This, in comparison to the reverse, (1) better-matches intuition (whereby it is more usual for something to start small and work its way up, than vice-versa), (2) discourages resource-waste (as the users of such apparatuses will be able to more easily tell whether the lower setting(s) is/are sufficient), and (3) facilitates machining (as if a setting is too small, the work can easily be redone with a larger setting; while the reverse is never the case.).
For cyclical systems that allow retrograde cycles, the default cycle (insofar as such a condition may be considered applicable) should be smallest-to-largest and, if applicable, clockwise.
Some examples of this: fan-pulls increase fan speed, and leather punches (when rotated clockwise) move from smallest-to-largest.
Although this may, at first glance, appear to conflict with the Theodian language's preference for large-to-small ordering; there is, in fact, no conflict; as these two order-preferences apply to wholly different phenomena, whose primarily similarity lies in the simple fact that a size continuum can be used to term them. An unrelated situation in which there is an ideal size order that differs from that of round-robin systems, is in gauging material: it is better that the material start out thicker than necessary, as it can always be planed down; whereas the reverse is typically far more difficult.
Other
- Addresses & phone numbers
Addresses and phone numbers are unified, and stored in the form of myriadic numerical codes. Each segment of such a number (excepting the last, optional segment, which is shorter) is, accordingly, 4 digits long, and can hold up to 20,736 values. Matching myriads (blocks of 4 digits) can be omitted when entering an address or phone number into a properly programmed geographically aware device. One's address only very rarely changes. The myriads represent the following things (items with an asterisk (*) are to be arbitrarily determined): country*, supercluster, galactic cluster, galactic sector*, star system, satellite, region*, greater municipality*, city sector*, building. Within each building, there is an additional subdomain of three digits allowing for a total of 1727 total phone numbers per building. These three digit codes are also to be used for room numbers; leftover ones can be used for excess telephone numbers, starting from the top (333) rather than the bottom (1). Buildings requiring more numbers will have to host their own sub-directories. Having numbers work in this way not only allows for the omission of redundant myriads (as previously mentioned), but also for shorter numbers to remain unambiguous to processing-software, as whenever the total number of digits is not divisible by 4, the leftover digits will be the ones at the end of the number.
The lowest floor of a building is always floor #1. There are no superstitions regarding the 4th, 13th, etc floors. Originally, 0 was the ground floor, and floors below that were negative numbers, while floors above that were positive numbers. However, this didn't work with the addressing scheme above, and could regardless be ambiguous for structures with multiple ground-level floors.
There are reserved numbers for public services. These are all 3 or fewer digits in length, and are all prefixed by 0 (which never occurs at the beginning of any other not-myriadic). This will redirect the call to the most local public facility indicated by the three-digit code entered. Most of these numbers will be reduplicative or very simple, like 033 or 05.
Every unique myriad (with the exception of shorthand public numbers) also receives a nickname to make frequently talking about a locale more efficient (Due to the nature of human short-term memory, naming each myriad will allow more data to be temporarily stored than could be achieved with raw numbers.). These are democratically decided by the populace in their respective areas, and must be a single non-compound word, as well as unique among the other 20,736 numbers at its tier.
- Books
Theodian books open horizontally from right-to-left, just like English books. However, this orientation is ideal not for LtR-vertical writing systems (where it creates two columns) like Latin, but for vertical-LtR writing systems (where it creates a single column and is more akin to reading a webpage) like Theodic. Probably the most comfortable way to hold a book, however, is bottom-to-top (as gravity turns the next page for you), which is ideal for horizontal-BtT writing systems, like Latin; but there are a number of drawbacks with these sorts of systems relative to a vertical-horizontal system like Theodic, which make the former ultimately undesirable, especially with the increasing replacement of books by e-media.
This particular book-orientation is also ideal for right-handed use. When the left hand is used to steady the book, this allows one to initiate a page-turn more quickly than with a book opening left-to-right, as the right hand would here rest along the page to be turned. For a right-handed person, this hand-configuration is likely more comfortable than holding the book with the right hand, and turning the page with the left hand (which would be ideal for lefties and left-to-right book-turning).
- Colour
The basic colours in Theodia are red, orange, yellow, green, cyan, blue, and magenta -- the primary colours of the CMY and RGB models, plus orange -- and black, grey, and white -- totalling 10 basic colours. These basic colours are often combined with one-another to derive intermediate shades; and "light" and "dark" are often used, as well.
In order to maximize accessibility for the colourblind, any red-green differences used in other countries are, in Theodia, replaced with magenta-green distinctions; as not only are magenta and green opposite hues on a CMY/RGB wheel, but they also provide extremely comfortable colouration and contrast to all three categories of non-monochromatic colourblind. This results from magenta's being an even mixture of blue and red (meaning that lacking one or the other hue does not prevent magenta from being perceived), and from green's being in the middle of the human visible spectrum (meaning that it's the most reliably saturated archetypal hue). To a non-colourblind person, magenta-green is rendered as azure-yellow through a protanopic filter, azure-tan through a deuteranopic filter, and pink-cyan through a tritanopic filter. Where a third colour is needed with an otherwise magenta-green scheme, the desaturated colours white, black, and grey are recommended.
- Power outlets

In Theodia, the power outlets are similar in appearance to those used in Australia and China, and similar in regulation to those in the UK.
- The basic specifications are as follows:
- Power-plugs are male and wall-outlets female because the alternative would make it very easy to electrocute yourself.
- Pins are straight and linear. Unlike perfectly round pins, linear ones can be orientated -- a useful way to prevent incorrect plugging.
- All three pins are ultimately identical in construction. This simplifies manufacturing.
- The pins are rounded. This minimizes sparking.
- The pins are arranged in an upside-down triangle. This provides more stability than other orientations.
- The top two pins are rotated such that they together form a chevron. This not only provides additional stability, but makes it impossible to invert a groundless plug's polarity without tinkering.
- The bottom pin is vertical. This provides superior vertical stability relative to a horizontal pin.
- When looking at an upside-up power-outlet mounted on a wall, the rightmore pins carry negative charge, and the leftmore pins carry positive charge. This is the safest orientation because (1) a plug is typically held between thumb and forefinger, (2) the thumb is more likely to extend past the base of the plug, (3) most people are right-handed, (4) right-hand thumbs are on the left of the hand, and (5) electricity flows from negative to positive; essentially, this puts the active contact at a maximal distance from the skin.
- Safety regulations are as follows:
- Sockets must be shuttered. This makes accidental electrocution difficult.
- The ground-pin opens the shutters, and must therefore be longer than the polarized pins. This also means that the ground-pin is always the first and last pin to be connected, which again improves safety. This also means that all plugs must have a ground pin.
- All outlets must have their own fuse and a user-accessible breaker. This helps protect appliances and makes it possible to shut appliances off without needing to unplug them.
- The bases of the polarized pins must be covered in an electrical insulator. This prevents accidental electrocution during insertion and removal.
- Supplemental (recommendary) specifications are as follows:
- Wall-plates should have a slot for a screw so that cords may be more securely attached to the wall when necessary. The plug-mounted screw mechanism itself is optional and up to the manufacturer.
- Wall-plates should arrange their outlets horizontally (landscape, instead of portrait). This prioritizes vertically extended cords, which are stabler under gravity than horizontally extended cords.
- Cords should extend from their plugs downwards, not outwards, upwards, or sidewards. Having cords in an orientation harmonized with that of their wall-plate (which is, in this case, landscape) makes it easier to use, ie, power-strips, because cords will not cover other outlets. Not having cords extend outwards makes it easier to place furniture against the wall and harder to accidentally unplug something by pulling on the cord. Having all cords extend downwards is more stable under gravity than having them extend upwards, and allows easier access to the outlet's breaker and screw, as these can then be located above the outlets.
- Plugs should not be wider than the width of a typical outlet. This prevents plugs being so wide that they prevent usage of other outlets.
- Wall-outlets should be flush with the plate, as this allows for much looser tolerances on the shapes of plugs.
- Magnetism
The poles of a magnet are referred to as + and - instead of "north" and "south". This is because (1) the magnetic poles of planets, stars, etc occasionally invert; and (2) magnetic poles do not have to align with rotational poles. Using cardinal directions to name magnetic poles inevitably results in "north" being south and "south" being north for some objects in Space. Using + and - avoids this issue.
- Music
The musical temperament most commonly used in Theodia is a 12-TET with a different set of frequencies than used in the Western world, these being derived from Ergonometric units. This particular temperament was chosen after weeks of research, and happens to be one of the places where the world already has a relatively "optimal" system. Equal temperaments avoid wolf-intervals and permit infinite regular transposition; and 12, also Theodia's mathematical base, is often considered the best base for day-to-day human use.
As well, Theodian instruments traditionally have their primary notes tuned to a hexatonic whole-tone scale. This was seen as the ideal tuning, as 6's being half of the temperament (12) results in all sharps and flats being identically actuated at different parts of an instrument, thus making transposition symmetrical (isomorphic). This also results in all asymmetrical scales being more-or-less equally difficult; unlike in Western tuning, where one particular iteration of diatonic tuning is particularly easy, but others very complex. It also makes the numbering of notes more regular, and the underlying musical theory a little more transparent.
Although instruments are typically tuned to a hexatonic scale, most music is played in one of many heptatonic and pentatonic scales, as whole-tone scales, although infrastructurally ideal, don't leave much room for the differentiation necessary for melody. The "default" scale in Theodia is the heptatonic diatonic scale, like in Western music, due to its being a repeatable pattern generated by a circle of fifths, easy conversion to a minor scale, large number of available notes, and the presence of several pentatonic scales within it.
The ways in which current Theodian musical transcription varies from typical Western transcription, is that there are six horizontal lines in an octave, and the notes are numbered 0-3 (instead of A-G with sharps and flats). The frequency of the lowest conventional note is yet undetermined. A single octave of the major diatonic scale, starting from C, is numbered as such in Theodia: 0245793.
Swena is looking to create a wind instrument that can be played when breathing in either direction, a stringed instrument that works well bowed and strummed, and a percussion instrument that works well with finger tapping. The stringed instrument will likely be a variation of a 12-stringed harpejji.
See also
References
- ↑ http://www.ncbi.nlm.nih.gov/pubmed/18841414
- ↑ http://qjmed.oxfordjournals.org/content/qjmed/89/2/109.full.pdf
- ↑ http://www.komci.org/GSResult.php?RID=0137JKSCT%2F2013.11.2.114&DT=1
- ↑ https://en.wikipedia.org/wiki/Atmospheric_pressure#Mean_sea_level_pressure
- ↑ http://www.phonearena.com/news/Report-7-inch-tablets-are-the-most-popular-size-for-Android-users_id41860
- ↑ https://www.sundoginteractive.com/blog/why-16-9
- ↑ http://pocketnow.com/2015/11/20/world-most-popular-mobile-screen-size-resolution
